Glossary

Boundary Conditions@

Periodic Boundary Conditions @

Periodic boundary conditions (PBC) are used to simulate a large (infinite) system by using a small part called a unit cell, which is a finite representative volume element of an infinite system. When an object passes through one side of the unit cell, it reappears on the opposite side. Hence, a simulation cell with PBC can be considered as being surrounded infinite number of unit cells called Images.

Coordinates of the particle that crosses the simulation box boundary, are given as

\[ \begin{equation} x_{A}^{\prime}=\left[\begin{array}{ll}{x_{A}-L,} & {x_{A}>L} \\ {x_{A}+L,} & {x_{A}<0}\end{array}\right] \end{equation} \]

where $x_A$ is the x-coordinate of the particle after moving, $X_A'$ is the "image" coordinate, $L$ us the liner size of the cell [1]

For more information please refer to wikipage on PBC

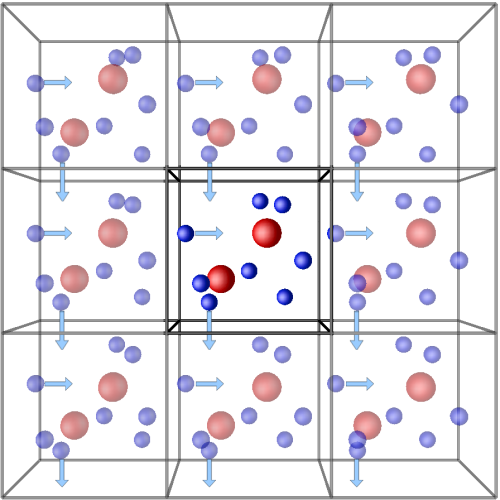
Figure.1 Schematic representation of the idea of periodic boundary conditions.(Courtsey: ISAACS Program)

Finite Boundary Conditions @

In KSOME, finite boundary conditions (FBC) can be applied to mimic the effect finite size of grain.

Absorbing Boundary Conditions @

When an object crosses the simulation box boundary then they are removed from the simulation

References@

A. M. Ovrutsky, A. S. Prokhoda, M. S. Rasshchupkyna Computational Materials Science: Surfaces, Interfaces, Crystallization Elsevier

Defect Cluster Sizes@

Void Size@

$\frac{4\pi}{3}R^3 = n\Omega$ after rewriting, $R = \bigg(\frac{3n\Omega}{4\pi}\bigg)^{\frac{1}{3}}$, where $\Omega$ = atomic volume, $n$ = number of point-defects in the cluster or cluster size. For BCC and FCC lattices, $\Omega$ = $\frac{a_0^3}{2}$ and $\frac{a_0^3}{4}$, respectively.

Loop Size @

$\pi R^2b = n\Omega$, where $b$ = Burgers vector. After rewriting, $R = \Big(\frac{n\Omega}{b\pi}\Big)^{\frac{1}{2}}$.

Distance of a point from a surface@

The distance (d) of a point $P = (x_0, y_0, z_0)$ to a plane determined by the equation $Ax+By+Cz+D=0$ is given as in the figure below

Example

$Z=100$ is the equation of an $XY-$Plane bold to $z-$axis at $z=100$. For this plane, $C=1~ \&~ D=-100$. Then the distance of the point $P(x_0,y_0,z_0) = (5,5,5)$ from the plane is

$$ d = \frac{|0(5)+0(5)+1(5)-100|}{(0+0+1)^{½}}=95 $$

Eq. of a plane with a bold vector N = (A, B, C) and Q = (x₀, y₀, z₀)@

The equation of the plane N is given as

\[ \begin{eqnarray} A(x-x_0)+B(y-y_0)+C(z-z_0) = 0~\text{can be written as}\label{Eq_Plane1}\\ Ax+By+Cz+D=0,\text{ where } D = -Ax_0-By_0-Cz_0 \label{Eq_Plane2} \end{eqnarray} \]

Glossary

Boundary Conditions@

Periodic Boundary Conditions@

Finite Boundary Conditions@

Absorbing Boundary Conditions@